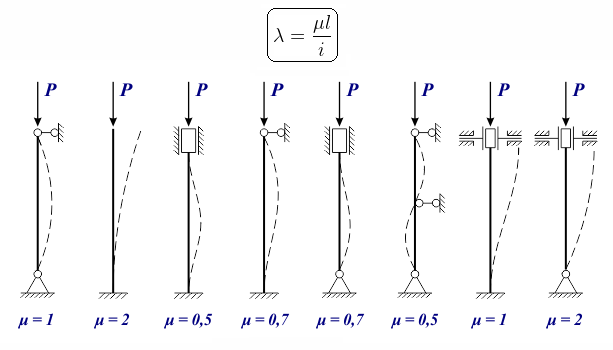
P – сжимающая сила;

ℓ – длина стержня;

i – радиус инерции сечения;

μ – коэффициент приведения длины, зависящий от условий закрепления стержня;

λ – гибкость стержня.

Если стержень в разных плоскостях имеет различные радиусы инерции или различные условия закрепления, то в расчетах используется наибольшее значение гибкости.

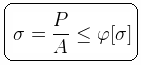
A – площадь сечения;

[σ] – основное допускаемое напряжение на сжатие;

φ – коэффициент снижения основного допускаемого напряжения (коэффициент продольного изгиба), зависящий от гибкости λ и материала стержня:

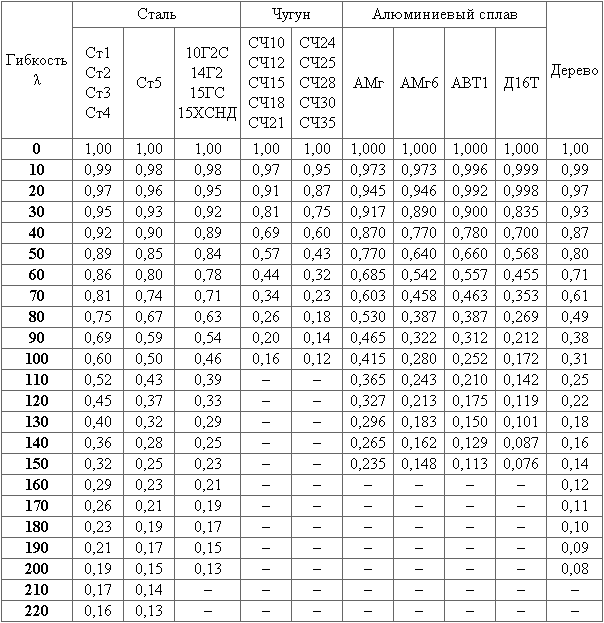
В строительстве для сталей коэффициент продольного изгиба φ задается в зависимости от гибкости λ и расчетного сопротивления R_y (СНиП II-23-81*):

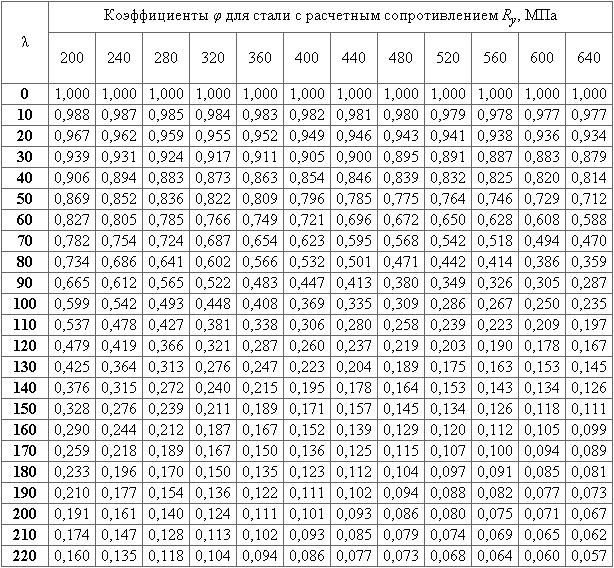
Если для материала нет справочных значений φ, или необходимо определить реальный запас устойчивости, то используется условие устойчивости в виде:

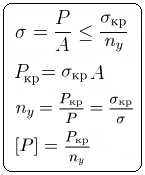
n_у – запас устойчивости;

P_кр – критическая сила;

[P] – допускаемое значение сжимающей силы;

σ_кр – критическое напряжение, которое для стержней малой гибкости равно пределу текучести σ_T, для стержней средней гибкости определяется по формуле Ясинского, для гибких стержней – по формуле Эйлера:

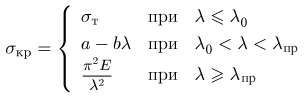
E – модуль упругости материала;

λ₀ – максимальное значение гибкости, при котором допустимо не учитывать эффект потери устойчивости (достаточно простого расчета на сжатие);

λ_пр – минимальное значение гибкости, при котором применима формула Эйлера;

a, b – коэффициенты формулы Ясинского.

Для чугуна формула Ясинского имеет вид: σ_кр = a – bλ + cλ².

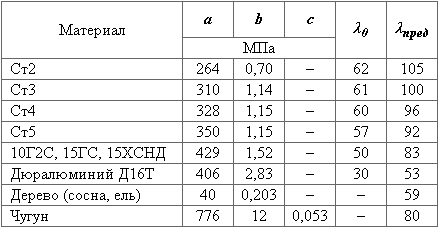
Для стержней средней и малой гибкости критическое напряжение можно (если, например, для материала отсутствуют справочные данные для формулы Ясинского) определить по параболическому закону:

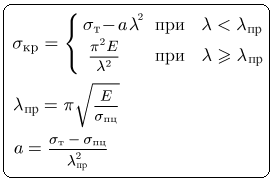
σ_пц – предел пропорциональности;

a – коэффициент, определяемый из условия сопряжения с кривой Эйлера.

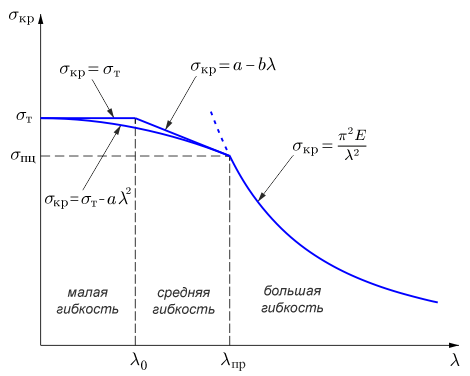
Для хрупких материалов в формулы для определения критического напряжения вместо предела текучести σ_T подставляют предел прочности на сжатие σ_В.